 |
|
|
|
 |
|
|
The Two-Clock Problem
Storrs McCall (Department of Philosophy, McGill University)
This is analogous to, but not identical with, the twins paradox. In its "three-clock" form, the twins paradox in flat spacetime involves clock 1 following an inertial path from A to C, clock 2 an inertial path from A to B, and clock 3 a third inertial path from B to C. If clocks 1 and 2 are synchronized at A, and 2 and 3 are synchronized at B, clock 3 will record a total elapsed time at C which is less than that of clock 1. This demonstrates that triangles in Minkowski geometry with timelike sides obey a law of triangle inequality opposite to that in Euclidean geometry. The sum of the lengths of AB and BC is less than that of AC.
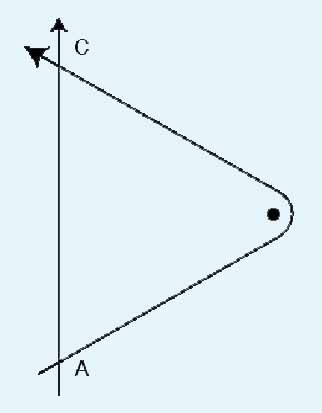The two-clock problem also involves two clocks synchronized at A. Clock 1 follows an inertial path from A to C in flat spacetime, far away from massive bodies. Clock 2 starts off on an inertial path at an angle to AC, coasts around a massive body at B without rocket power, using the slingshot effect, and rejoins clock 1 at C (see figure). Both the paths of the two clocks are geodesics. When the clocks are compared at C, will clock 2 record (i) more total elapsed time than clock 1, or (ii) less time (as one would expect from the twins paradox), or (iii) the same amount?
I am sure this result is recorded somewhere in the literature, but I don't know where.
|
|
|
 |
|
 |